Вейвлет-преобразование заключается в разложение исследуемого сигнала в ряд базисных функций, имеющих специальные свойства. Все функции определенного базиса являются подобными и отличаются только масштабными коэффициентами. Каждая функция базиса имеет свою частоту и локализацию. Волновые базисные функции должны обладать определенными свойствами: интегрируемости и нулевого среднего. Свойство интегрируемости заключается в том, что интеграл по бесконечности от квадрата модуля волновой функции имеет конечное значение. Свойство нулевого среднего требует, чтобы интеграл по бесконечности волновой функции был равен нулю.
Непрерывное вейвлет-преобразование определяется как:
![]()
Где: g(,t) - волновая функция, - означает комплексное сопряжение, x(u) - сигнал.
Наиболее широко используется волновая функция Морлета (Morlet’s wavelet), определяемая как:
![]()
Следовательно, можно записать:
![]()
Преобразование Фурье равенства (3) является симметричной функцией относительно частоты 0/2a. Поэтому wavelet-преобразование можно рассматривать как частотно-временное с частотой анализа равной 0/2a. Среди множества известных на данный момент волновых функций функция Морлета обладает следующими отличительными свойствами:
Определяется точной аналитической функцией.
Проста для вычисления.
Ее применение ведет к квазинепрерывному представлению.
![]()
Любая функция, используемая в качестве волновой функции, должна удовлетворять следующему необходимому условию:
В случае функции Морлета это условие выполнимо для широкого диапазона значений 0.
Другой подход основан на фиксации 0 и модификации g(t) введением дополнительного параметра , что приводит к модифицированной волновой функции:
![]()
![]()
Таким образом, выбирая малые значения (1) - что соответствует высокой концентрации энергии во временной области - получают низкое разрешение в частотной области и, наоборот, большие значения (2) приводят к более высокому разрешению в частотной области (принцип неопределенности). Принимая во внимание это утверждение, для пары значений (1 и 2) определено модифицированное вейвлет-преобразование, имеющее размерность энергии. Его можно записать как:
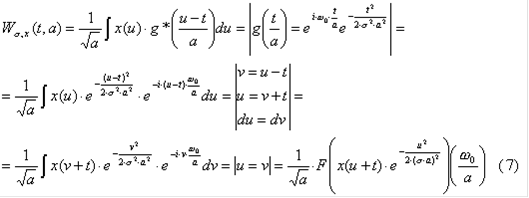
где F означает Фурье оператор.
![]() и высокое частотное разрешение.
и высокое частотное разрешение.
Для данного значения a (связанного с частотой) параметр определяет ширину Гаусового окна. Малые значения улучшают временное разрешение в ущерб спектральному, и наоборот. Интуитивно понятно, что произведение (7) принимает большие значения только тогда, когда оба множителя значительны. Таким образом, получается высокое временное разрешение,
Чтобы получить центральную частоту волновой функции равную 1 Гц при a=1, мы должны принять 0=2 rad/s. В классическом волновом преобразовании параметр a изменяется согласно закону: a=2-. Если целое, закон называется двоичным. Из равенства (3) следует, что центральная частота также подчиняется двоичному закону, что несовместимо с классическим частотно-временным распределением.
Следовательно, можно переписать определение этого параметра как:
![]()
где f - интервал дискретизации по частоте, а n - положительное целое.
Советуем почитать:
Узлы формирования и обработки первичных сигналов Современные УЗ сканеры являются сложными многофункциональными устройствами. Они позволяют выполнять исследования в реальном масштабе времени в режиме М и режиме В, а так ...
Импульсный лабораторный источник питания Для проведения лабораторных работ, исследований и испытаний приборов необходим источник питания. Требования к источникам вторичного питания, предъявляются очень высокие. Особенно к таким ...
Измерение плотности потока энергии СВЧ излучения Целью работы является: ознакомление с методами и средствами измерения плотности потока энергии СВЧ излучения, установление соответствия исследуемой микроволновой печи всем требованиям пр ...