После выделения тонов сигнал не пригоден для классической фильтрации с целью удаления шума, так как полезный сигнал расположен в одной с шумом частотной области. Отличие состоит в амплитуде сигнала и шума. В этой связи жесткая пороговая обработка вейвлет-кодером является наиболее оптимальным решением. Удаление шума позволит не только сделать сигнал “более читаемым”, но и обеспечит возможность его оптимальной компрессии за счет удаления последовательности нулевых коэффициентов разложения. Однако, кроме “стандартных” достоинств применения вейвлет-метода положительным для работы с сигналом оказалась возможность автоматического выделения “истинных” тонов Короткова, что на практике так или иначе выполняется. Полученный эффект достигнут за счет правильного выбора величины порогов обработки коэффициентов разложения. На рис.11 представлен исходный сигнал тонов. Виден шум.
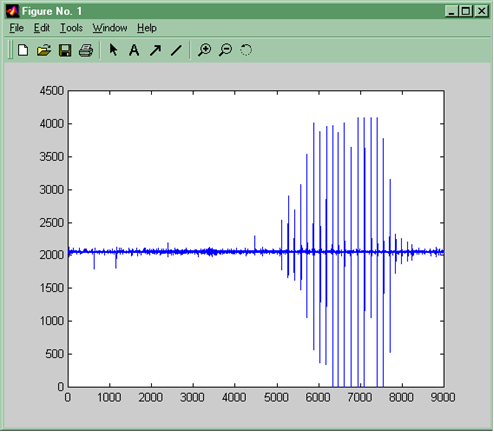
Рис. 11. Исходная запись тонов Короткова.
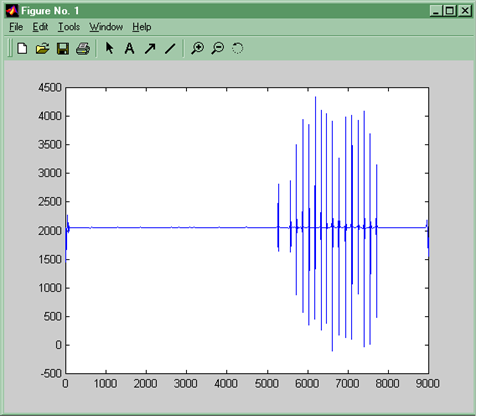
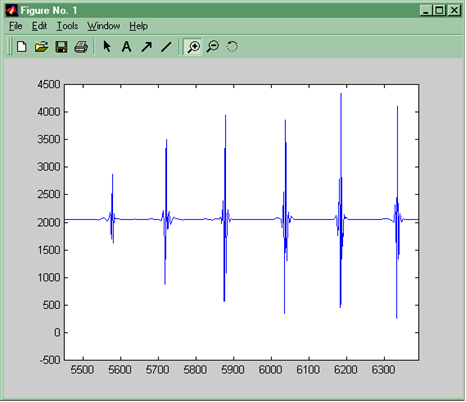
Рис.12. Тоны Короткова после обработки. Присутствуют только “истинные” тоны при отсутствии шума в сигнале
После пороговой обработки коэффициентов разложения оставлены только “истинные” тоны (рис.12).
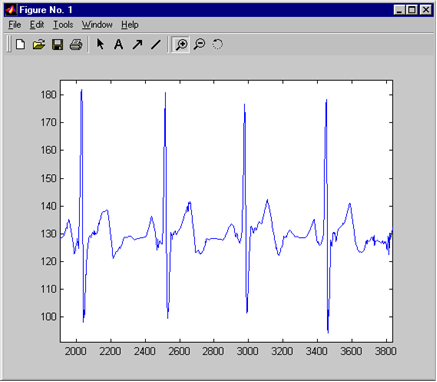
Рис.13. Сигнал кардиограммы до и после обработки вейвлет-кодером.
Советуем почитать:
Волоконно-оптические кабели ...
Разработка цифрового измерителя кровяного давления на микроконтроллере MC68HC908JL3 С развитием микроэлектронной индустрии, а в частности с развитием микроконтроллеров, появилась возможность делать малогабаритные и сравнительно дешёвые электронные изделия. На сегодня ...
Определение безотказности РЭУ при наличии резервирования замещением (резерв ненагруженный) Целью данного курсового проектирования является получение (расчетным способом и моделированием отказов на ЭВМ) и сравнение показателей безотказности РЭУ при наличии резервирования замещение ...