Любое логическое выражение, составленное из n переменных с помощью конечного числа операций алгебры логики, можно рассматривать как некоторую функцию n переменных. Двоичная функция может принимать только два значения: 0 и 1 – в зависимости от значений переменных. Такие функции являются удобным инструментом для описания, анализа и синтеза переключательных схем (бесконтактных и контактных), поэтому они называются переключательными функциями (ПФ).
Для ПФ n переменных x0,…,xn-1 будем использовать обозначение y (x0,…,xn-1). Совокупность значений переменных, в которой каждая переменная может принимать значения 0 или 1, называется набором. Любая функция n переменных может быть определена на 2n наборах. Это следует из того, что каждому набору соответствует n-разрядное двоичное число, а количество различных двоичных чисел при n разрядах равно 2n.
Существуют несколько способов задания ПФ.
1. Табличный, когда функция задается в виде таблицы истинности (соответствия). Таблица истинности содержит 2n строк ( по числу наборов), n столбцов значений аргументов и один столбец значений функции. В таблице каждому набору аргументов соответствует значение функции.
Таблица истинности ПФ, значения которой соответствуют значениям, принимаемым большинством переменных в наборе (функция голосования), определяет ПФ мажоритарного элемента “два из трех” (переноса двоичного разряда.
2. Координатный способ, когда функция задается в виде координатной карты состояний, например в виде карты Карно. Карта содержит 2n клеток по числу наборов значений переменных. Каждая клетка задается координатами строки и столбца, соответствующими определенному набору. Все аргументы разбиваются на две группы так, что одна группа определяет координаты строки, а другая – столбца. Порядок записи значений переменных в каждой группе задается записью переменных в соответствующем порядке над столбцами и около строк. Кодовые комбинации, задающие координаты двух соседних столбцов (строк), соответствуют двум соседним кодовым комбинациям циклического кода Грея .Соседние комбинации такого кода отличаются значениями только одной переменной. Значение функции на данном наборе проставляется внутри клетки (клетки, соответствующие нулевым значениям ПФ, часто в целях наглядности оставляют пустыми).

На рис. 1,а приведена карта Карно для ПФ мажоритарного элемента “два из трех”, заданной таблицей истинности 2, на рис.1,в – для ПФ компаратора. На рис.1,б,г в клетках проставлены их номера, соответствующие номерам наборов.
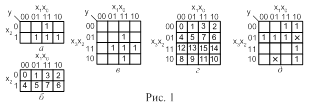
Карты Карно являются важным средством проектирования логических схем. Особенность карт в том, что любые две соседние клетки отличаются значением какой-либо одной и только одной переменной. Эта особенность характеризует также клетки первой и последней строк, первого и последнего столбцов, поэтому такие клетки тоже можно считать соседними. Указанная особенность соседних клеток позволяет легко осуществлять упрощение ПФ посредством использования тождества склеивания.
3. Числовой способ, когда ПФ задается в виде десятичных номеров тех наборов переменных, на которых функция принимает значение 1. При этом следует учитывать, что i-я двоичная переменная имеет “вес” 2i. Например, приписывая переменным x2,x1,x0 соответственно “веса” 22,21,20, в числовом виде ПФ рис.1,а будет задана как y( x2,x1,x0 ) = ![]() ( 3, 5, 6, 7 ).
( 3, 5, 6, 7 ).
Можно использовать для задания функции десятичные номера наборов, на которых функция принимает значение 0. Та же ПФ (рис.1,а) в таком случае будет задана как y( x2,x1,x0 ) = ![]() ( 0, 1, 2, 4 ).
( 0, 1, 2, 4 ).
4. Аналитический способ, когда ПФ задается в виде алгебраического выражения (структурной формулы), получаемого путем применения логических операций к аргументам ПФ. Следует учитывать, что одну и ту же ПФ можно задать в виде разных структурных формул, которые отличаются друг от друга выбором используемых логических операций и своей сложностью.
При использовании всех n аргументов для записи алгебраического выражения существует две формы структурных формул.
Совершенная дизъюнктивная нормальная форма (СДНФ) представляет собой дизъюнкцию минтермов.
Минтерм (минимальный терм, конституента единицы) есть логическое произведение всех переменных ПФ для наборов, на которых ПФ принимает значение 1.Если в наборе переменная равна 1, то в минтерм эта переменная входит без инверсии, если равна 0 - то с инверсией. Например, если на наборе x2 = 0, x1 = 1, x0 =1 ПФ принимает значение 1, то соответствующий минтерм m3 для третьего набора будет иметь вид m3 =![]() x1 x0 . Перейти на страницу: 1 2
x1 x0 . Перейти на страницу: 1 2
Разработка мероприятий по повышению эффективности деятельности ОАО Московская Городская Телефонная Сеть Актуальность темы. В настоящее время активно развивается коммерческий сектор телекоммуникационного рынка России, представленный на региональных рынках как мультисервисными, так и с ...
Система дублирования видеопотока в компьютерном классе Разработка дипломного проекта является завершающим этапом обучения в техникуме, который показывает, какого уровня специалист подготовлен в результате обучения. Это сложная многогранная р ...
Микропроцессорная система на базе комплекта КР580 В данном курсовом проекте рассмотрен микропроцессорный комплект серии КР580. Этот набор микросхем, аналогичен набору микросхем Intel 82xx. Представляет собой 8-разрядный комплект на осн ...