Дизтерм (дизъюнктивный терм) – результат склеивания соседних макстермов, входящих в подкуб (соседних нулевых клеток). В алгебраическом представлении дизтерм - есть дизъюнкция переменных, имеющих неизменное значение в координатах строк и столбцов всех объединяемых клеток; если неизменное значение переменной в координатах равно 1, то в дизъюнкции она записывается с инверсией, если равна 0 – то без инверсии.
Для ПФ y9 (рис.3,ж) построенные подкубы имеют следующие дизтермы: 
МКНФ – есть конъюнкция дизтермов.
Пример: МКНФ для ПФ y9 (рис.3,ж) как результат минимизации по нулевым значениям функции имеет вид:
(
) (
) (
). (6)
Ранги контермов или дизтермов, которые входят в логическое уравнение МДНФ или МКНФ переключательной функции, в общем случае не одинаковы.
Общие правила минимизации функций, справедливые для любого числа логических переменных:
- прямоугольные области карты Карно, составляющие подкубы, могут состоять из 1, 2, 4, 8, 16 и т.д. только единичных клеток (при получении МДНФ) или только нулевых клеток (при получении МКНФ);
- для подкубов выбирается минимальный вариант их построения на карте Карно, при котором число подкубов минимально, а их размеры максимальны;
- клетки карты Карно могут неоднократно входить в разные подкубы, если это необходимо для увеличения их размеров и уменьшения их количества.
При минимизации неполностью определенных функций факультативные клетки, обозначенные на карте знаком 
, могут включаться в подкубы соседних клеток в тех случаях, когда позволяют сформировать
подкуб либо большего размера, либо такой, который охватит клетки, ранее не включенные ни в один подкуб. Включение клеток со знаком в подкубы соответствует доопределению функции на соответствующих этим клеткам наборах.
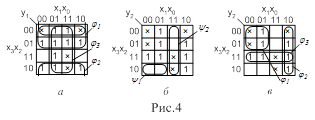
Формирование подкубов с включением в них факультативных клеток позволяет получать более простые, как правило, структурные формулы МДНФ или МКНФ. Минимизация функции 
, приведенной на рис.4,а, отличающейся от функции 
(рис.3,е) только наличием факультативных клеток, показывает, что включение клеток со знаком в подкубы позволяет получить выражение функции:
, (7)
которое существенно проще, чем (5) или (6). Существенное различие в сложности формул может иметь место и при минимизации неполностью определенной логической функции при использовании единичных клеток и нулевых клеток (МДНФ и МКНФ). Для функции 
, приведенной на рис.4,б, объединение нулевых клеток в подкубы 
и 
дает минимизированное выражение (МКНФ): 
= (
) (
). МДНФ для функции (рис.4,в) сложнее: 
= 
. Перейти на страницу: 1 2 3
Содержание кабеля под воздушным давлением Все магистральные и межстанционные кабели емкостью от 100 пар и более устанавливают под постоянное избыточное воздушное давление. Это делают во избежание проникновения влаги и дл ...
Система автоматического регулирование температуры теплоносителя зерносушилки Техническое задание на проектирование включает в себя исходные данные, позволяющие произвести синтез системы. К ним относятся функциональная схема нескорректированной САУ, сведения о при ...
Разработка датчика сетки частот генератора сигналов низкой частоты Измерением называется физический опыт, в результате которого находят численное значение измеряемой физической величины. Измерения являются важнейшим этапом деятельности работников всех ...