Если задан двоичный 88-разрядный код (11 байт), то при записи его в двоично-1024-ричном виде, получится 9 символов (8 символов по 10 бит и 1 символ из 8 бит). Т.е. исходные 88 двоичных разряда разбиваются на 9 групп по 10 разрядов. Каждую группу назовём 1024-ричным символом.
Код будет обнаруживать 3 ошибки (на 9 двоично-1024-ричных разрядов), т.е. кодовое расстояние ![]() .
.
Сначала определим правило нахождения контрольных символов. Если записать в виде таблицы информационные разряды, то можно заметить, что три контрольных символа рассчитываются по соответствующим строкам (суммируются символы по модулю 32), три других – по строкам и один – по первым шести контрольным.
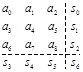
Рис. 2
Иначе говоря, ![]() ,
, ![]() ,
, ![]() ,(9)
,(9)
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Построим матрицу кодирования (образующую матрицу). Матрица кодирования будет содержать 9 строк (по количеству разрядов), левая часть матрицы содержит единичную матрицу Правая часть задаёт контрольные разряды:
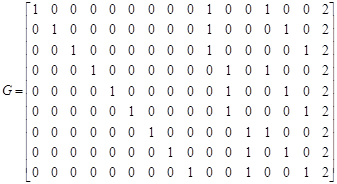 .(10)
.(10)
Перемножая вектор информационного кода на эту матрицу, можно получить вектор, в котором информационные и контрольные разряды разделены, число контрольных разрядов равно 7:
![]() .
.
Естественно, все операции должны выполняться по модулю 1024. Для проверки принятого кода на отсутствие ошибок требуется вектор умножить на проверочную матрицу. Проверочная матрица будет иметь следующий вид:
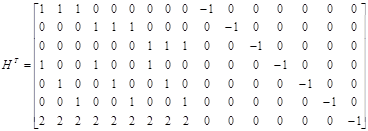 ,(11)
,(11)
где левая часть матрицы содержит транспонированную правую часть образующей матрицы. Проверка правильности кода примет вид:
![]() .
.
Таким образом, код состоит из 20 байт, из которых 9 контрольных и 11 информационных. Код обнаруживает до трёх ошибок, причём не в отдельных двоичных разрядах, а в символах по 10 разрядов.
Матрицы (10) и (11) описывают код (160,88). Нельзя сказать, что код получился оптимальнее, чем код Хемминга или БЧХ (по скорости кодирования), однако его преимущество – более высокая скорость передачи, за счёт усложнения формы сигнала и более полного использования линии связи. Недостаток полученного кода – сравнительно сложная схемная реализация.
Примеры кодирования-декодирования
Для примера рассмотрим кодирование последовательности
92 8E AA 9B A2 A5 9A 55 4B D2 B4.
Эта последовательность в двоично-1024-ричном виде будет выглядеть так:
1001001010.0011101010.1010100110.1110100010.1010010110.0110100101.
0101010010.1111010010.10110100.
Для выравнивания, добавим в конец ещё два нулевых бита. Перейти на страницу: 1 2 3
Советуем почитать:
Проектирование системы передачи цифровых данных В настоящее время очень развиты различные системы передачи данных, разработаны основные стандарты, на основе которых строятся реальные системы. В настоящей работе была осуществлена попыт ...
Усилительный каскад с общим эмиттером Полупроводниковые электронные устройства делятся на два больших класса: аналоговые и цифровые (дискретные). В основе классификации лежит возможность изменения в устройстве электрического ...
Расчет телекоммуникационной сети ГТС малой емкости Актуальность проблемы в настоящее время развития телекоммуникаций происходит в направлении создания рынка телекоммуникационных услуг, внедрения новых телекоммуникационных технологий, их ...