Для того чтобы из системы (1) найти функции ω(t) и μ(t), необходимо понизить степень системы, то есть избавиться от производных второго порядка. Для этого введем функцию Z(t)= μ'(t), получим систему вида:
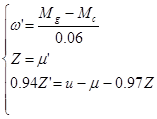 (2)
(2)
Решая систему численно, получаем табличные значения ω(t) и μ(t), по которым строим графики ω(t) (рисунок 2) и μ(t) (рисунок 3). По графикам хорошо видно, что ω(t) и μ(t) стремятся к равновесным значениям ω0=31.948 и μ0=0.5, ω(t)→ 31.948, μ(t) →0.5, что соответствует вычислениям.
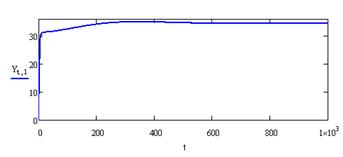
Рисунок 2 – График функции ω(t)
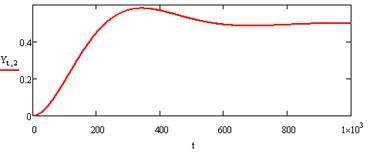
Рисунок 3 – График функции μ(t)
Советуем почитать:
Устройства регулировки и перемножения сигналов В усилителях необходимо регулировать усиление и форму АЧХ. Основные требования к регуляторам: 1) Минимум помех, вносимых регулятором (фон переменного тока, шумы трески и т.д.). ...
Измерительная техника и радиотехнические комплексы Производственная практика является важным этапом подготовки квалифицированных специалистов. Она является видом учебно-вспомогательного процесса, в ходе которого закрепляется теоретически ...
Проектирование устройства преобразования и воспроизведения музыкальных звуков Для определения необходимой архитектуры разрабатываемого программно-аппаратного средства, необходимо проанализировать цель и особенности его применения. Основной целью применения разраба ...