К этому классу относят в основном поверхности, образованные вращением кривых второго порядка.
1. Сферу образуют вращением окружности вокруг ее диаметра (рис. 3, б). Любая плоскость пересекает сферу по окружности. Очерк фронтальной проекции сферы называют главным меридианом, очерк горизонтальной проекции -экватором. Проекции точки К, лежащей на поверхности сферы, принадлежат проекциям горизонтальной окружности, проведенной на сфере.
Сфера образует форму диаграмм направленности антенны, обтекателя и излучателя антенны, головка микрофона, контактов реле, рукояток приборов и т. д. Сфера является поверхностью положения объекта в пространстве.
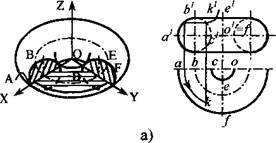
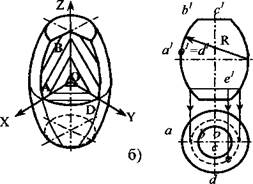
Рис. 4
кольцо, когда ось вращения 2. Круговой тор образуют вращением окружности вокруг оси, лежащей в плоскости этой окружности и не являющейся ее диаметром. Таким образом, сферу можно рассматривать как частный случай тора. Различают тор-не пересекает образующую окружность (рис. 4, а) и тор-бочку, когда есть такое пересечение (рис. 4, б). Тор-кольцо пересекается пл. ХОZ и УОZ по окружностям АВС и DЕF, а тор-бочка по окружностям АВ и СD. Пл. НОУ пересекает тор по одной или двумя окружностям, из которых СD называют горлом, а АF и АD -экваторами.
В радиотехнике используют также параболический и эллиптический тор.
Параболический тор образуют вращением параболы вокруг прямой, лежащей в плоскости этой параболы и не являющейся ее фокальной осью. Обычно за ось вращения берут прямую, перпендикулярную фокальной оси. На рис. 5, а дан случай, когда ось вращения не пересекает образующую параболу; на рис. 5, б ось пересекает параболу. Две координатные плоскости пересекают поверхность по одинаковым параболам; плоскость, перпендикулярная оси вращения, рассекает поверхность по окружности.
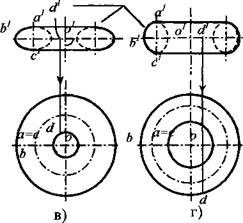Эллипс
Параболa
а)
б)
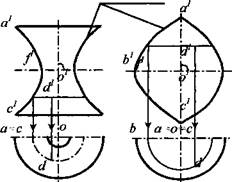
Эллиптический тор образуют вращением эллипса вокруг прямой, лежащей в плоскости этого эллипса и не являющейся его осью. Обычно за ось вращения берут прямую, перпендикулярную большой (рис. 5, в) или малой оси эллипса (рис. 5, г). Две координатные плоскости пересекают такой тор по эллипсам, третья - по окружностям.
Торовые поверхности имеют диаграмм направленности антенн, поверхности положения объекта в пространстве, антенны и их обтекатели, волноводы, резонаторы, громкоговорители, кулачки, сердечники катушек и т. д.
3. Эллипсоид образуют вращением эллипса вокруг его малой или большой оси. В первом случае получают сжатый (рис. 6, а), а во втором — вытянутый эллипсоиды вращения (рис. 6, б).
4.
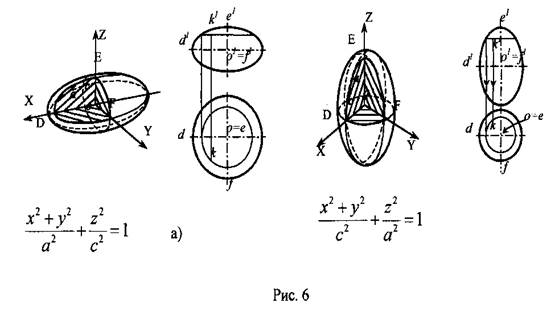
Пл. ХОZ и УОZ пресекают их по эллипсам DЕ и ЕF, а пл. ХОZ - по окружности DF.
Эта поверхность встречается при рассмотрении теоретических вопросов радиолокации и гироскопии; форму эллипсоида имеют зеркала антенн и лазеров, излучатели антенн, поверхности положения и т. д.
4. Двуполостной гиперболоид образует вращением гиперболы DЕ вокруг ее действительной оси FF1 (рис. 7, а). Пл. ХО2 и УО2 пересекают его по гиперболам DЕ и КЕ; пл. ХОY дает в сечении мнимую точку О.
5. Параболоид образуют вращением параболы ОD вокруг ее фокальной оси ОF (рис. 7, б). Пл. ХОZ. и YОZ пересекают эту поверхность по параболам ОD и ОЕ, а пл. ХОY дает в сечении точку О.
Зеркала антенн и лазеров чаще всего изготовляют
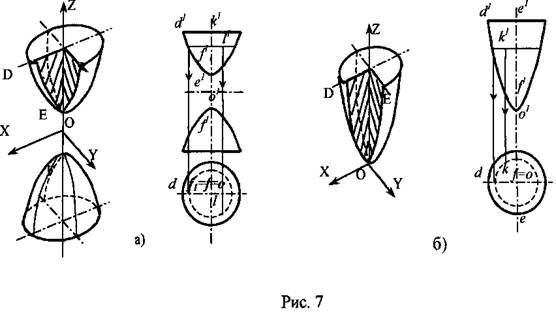
параболическими. Нередко зеркало антенны является сочетанием нескольких поверхностей. Так, антенна, предназначенная для дальней космической связи (рис.7, а), состоит из цилиндрического раскрыва 1, конического рупора 2 и параболического отражателя радиоволн 3. Фокус параболоида находится в точке Р.
6. Поверхность вращения общего вида образуют вращением произвольной кривой.
На рис. 8, б дана поверхность пространственной диаграммы направленности антенны локатора О, полученная вращением вокруг оси Z плоской диаграммы направленности СЮ РЕ. Объемные графики также часто имеют форму поверхности
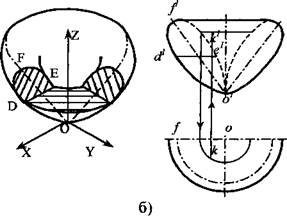
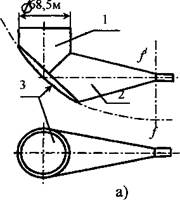
Рис. 8
вращения общего вида.
Поверхности с плоскостью параллелизма
Все поверхности этого класса - линейчатые.
1. Цилиндроид образуют перемещением прямой по двум кривым направляющим, когда образующая остаётся параллельной заданной плоскости.
2. Коноид образуют перемещением по кривой линии и прямой, когда образующая остаётся параллельной заданной плоскости. Частным случаем коноида является прямой геликоид, образуемый прямой по винтовой линии и её оси, когда образующая остаётся параллельной заданной плоскости. Перейти на страницу: 1 2
Советуем почитать:
Кривые линии и поверхности, их применение в радиоэлектронике и автоматике Кривые линии и поверхности их применение в радиоэлектронике и автоматике. Этот раздел курса имеет особое значение для графической подготовки инженера. Внешняя и внутренняя форма дета ...
Исследование и разработка программ расчета источников вторичного электропитания на ЭВМ Название темы дипломной работы "Исследование и разработка программ расчета источников вторичного электропитания (ИВЭ) на ЭВМ". Целью работы является исследование способов орган ...
Расчет телекоммуникационной сети ГТС малой емкости Актуальность проблемы в настоящее время развития телекоммуникаций происходит в направлении создания рынка телекоммуникационных услуг, внедрения новых телекоммуникационных технологий, их ...