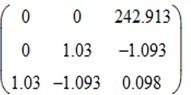Составим матрицу К:
Ранг матрицы K равен 3, что равно размерности системы (5), следовательно, система управляема.
Найдем коэффициент k0 регулятора замкнутой системы на границе устойчивости по критерию Рауса-Гурвица.
Сначала составим характеристическое уравнение для системы (6).
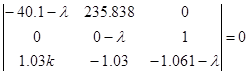
(7)
Найдем k по критерию Рауса-Гурвица.
Определитель Рауса-Гурвица составляется из коэффициентов характеристического уравнения и имеет свойство 
. где ∆n и ∆n-1 определители матрицы, an свободный член характеристического уравнения.
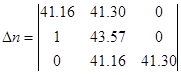
Проверим ∆1, ∆2:
∆1 = |41.16| = 41.16 > 0
∆2 = 
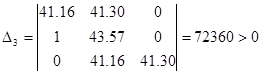
Условие границы устойчивости, если хотя бы один определитель будет равен нулю. Пусть ∆n=0, тогда аn=0. Получим:
, отсюда k0=0.169.
Система электронного управления магнитно-резонансного томографа МР томограф представляет собой сложную систему, состоящую из большого числа узлов различного назначения и размещенную на большой площади. Сказанное относится в первую очередь к МРТ ...
Структурные схемы цифровых радиопередающих устройств Радиопередающие устройства (РПдУ) применяются в сферах телекоммуникации, телевизионного и радиовещания, радиолокации, радионавигации. Стремительное развитие микроэлектроники, аналогов ...
Изучение показывающего и регистрирующего прибора ДИСК–250 Слесарь по КИПиА - это универсальный специалист, выполняющий работы по обслуживанию, ремонту и эксплуатации различного контрольно-измерительного оборудования и систем автоматического уп ...