В этом случае будет логичным делить координатные сигналы X = X+ – X– и Y = Y+– Y– на суммы их составляющих:
и 
(1)
При этом, кроме компенсации энергозависимости координатных сигналов, будут компенсироваться и погрешности за счет разброса резисторов координатной матрицы.
Представим координатные сигналы в виде сумм
; 
; 
; 
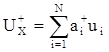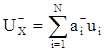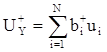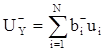, (2)
где N – число ФЭУ, ui - выходной (пороговый) сигнал i-го ФЭУ. Этот сигнал можно записать как ui = giE, где Е – энергия g-кванта , вызвавшего сцинтилляцию. Коэффициент gi в основном зависит от расстояния центра ФЭУ до места вспышки, а также от индивидуальных параметров ФЭУ. В принципе, его величина для определенных точек (тестовых, или реперных) может быть рассчитана. Подставляя в формулы (1) суммы (2), получим
; 
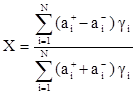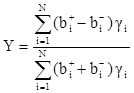. (3)
Как видно из формул (3), энергетическая зависимость координатных сигналов исключена. Теперь они в основном зависят от геометрических констант и электрических параметров (сопротивлений матриц и масштабных коэффициентов делителей). Кроме того, как уже отмечалось выше, погрешности в их вычисление вносит дискретность фотоприемников.
Если известны весовые коэффициенты ai , bi , то сопротивления координатной матрицы определяются по формулам
; 
; 
; 
, (4)
здесь R0 – сопротивление резистора в цепи обратной связи сумматора.
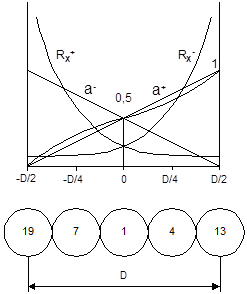
Наиболее простой способ определения весовых коэффициентов состоит в линейной аппроксимации их зависимости от координат. Рассмотрим, как это делается на примере группы ФЭУ, расположенных на оси X матрицы, состоящей из 19 ФЭУ (см. рис.3). Эта группа изображена на рис 5 Коэффициент а+ изменяется слева направо от нуля до единицы, а коэффициент а– наоборот – от единицы до нуля. Это значит, что левый крайний ФЭУ (3) не вносит никакого вклада в координатный сигнал Х+, а правый крайний (4) – в Х–. Весовой коэффициент ФЭУ, расположенного в центре (1), равен 0,12 Поэтому его вклады в сигналы Х+ и Х– будут одинаковыми и при их вычитании они компенсируются.
|
Сопротивления резисторов 
и 
определяются по формулам (3). На рис. 5 их графики имеют вид гипербол, зеркально отраженных относительно оси симметрии. При этом сопротивления для ФЭУ 13 и для ФЭУ 19 будут равны R0 , а для центрального ФЭУ все четыре весовых резистора будут иметь одинаковые сопротивления 2R0. Сопротивления и соответственно для ФЭУ 19 и 13 равны бесконечности, т.е. просто отсутствуют. Весовые сопротивления для ФЭУ 4 и 7 будут равны соответственно 4R0 и 4/3R0 , или 1,333R0. Из этого простого примера видно, что для координатной матрицы нужно брать высокоточные спротивления (не менее 0,1%).
Для оптимизации сопротивлений резисторной матрицы можно воспользоваться критериями минимума нелинейности пространственной зависимости координатных сигналов или минимума неоднородности изображения. Сущность первого метода состоит в минимизации суммы квадратов отклонений координатных сигналов от истинных координат сцинтилляций, вычисленных в нескольких тестовых точках, равномерно покрывающих площадь детектора. График коэффициентов а+, найденных этим методом, показан на рис.5 тонкой линией. Перейти на страницу: 1 2 3 4 5 6
Советуем почитать:
Измерительная техника и радиотехнические комплексы Производственная практика является важным этапом подготовки квалифицированных специалистов. Она является видом учебно-вспомогательного процесса, в ходе которого закрепляется теоретически ...
Проектирование системы передачи цифровых данных В настоящее время очень развиты различные системы передачи данных, разработаны основные стандарты, на основе которых строятся реальные системы. В настоящей работе была осуществлена попыт ...
Разработка микропроцессорной системы управления объектом Микропроцессорная система (далее МПС) предназначена для управления некоторыми объектами. Рисунок 1 - Структурная схема связи МПС с внешними объектами. Согласно рисунку ...