Можно дать несколько различных определений кривой линии как геометрическому образу. Одно из них: кривая линии есть траектория перемещающейся точки.
Если кривая линия совмещается всеми точками с плоскостью, ее называют плоской. Порядком плоской алгебраической кривой считают максимальное число точек ее пересечения с прямой линией. К плоским кривым относятся все кривые второго порядка, подробно изучаемые в аналитической геометрии. На рис. 1 показано построение этих кривых и приведены их канонические уравнения.
Эллипсом является геометрическое место точек М, для которых сумма расстояний до точек F1 и F2 постоянна и равна большой оси АВ (рис. 1, а). Точки F1 и F2 называют фокусами. Построим точку, принадлежащую эллипсу, если даны фокусы F1, .F2 и вершины А, В. Для этого на оси АВ берем произвольную точку L и из фокуса F1 проводим дугу окружности радиусом АL. Затем из фокуса F2 чертим дугу окружности радиусом ВL, пересекающую первую дугу в точке М. Таким образом, F1 М + F2М = АВ.
При равных осях эллипс превращается в окружность, являющуюся геометрическим местом точек плоскости, равноудаленных от данной точки О (рис. 1, б).
Параболой является геометрическое место точек М, для которых расстояния до точки F плоскости и до прямой КN, не проходящей через точку F, равны (рис. 1, в). Вершина О параболы делит расстояние от точки F до прямой КN пополам. Точку F называют фокусом, прямую КN -директрисой. Построим точку М, принадлежащую параболе, если дан фокус F и директриса КN. Для этого проводим прямую LМ II КN и из точки F засекаем ее дугой окружности радиусом МN. Итак, МN = МР
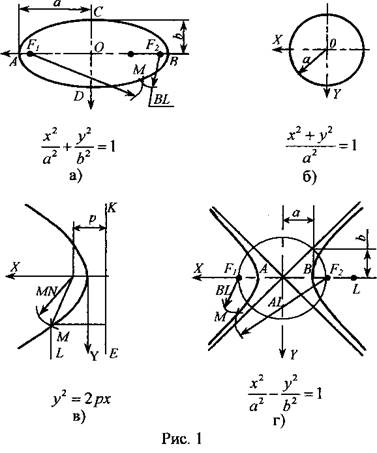
Гиперболой является геометрическое место точек М, для которых разность расстояний до точек F1 и F2 плоскости постоянна и равна расстоянию между вершинами А и В кривой (рис. 1,г)
Точки F1 и F2 называют фокусами, координатную ось X -действительной осью, а У - мнимой. Если даны вершины А, В и фокусы F1 и F2, то принадлежащую гиперболе точку строим следующим образом. На действительной оси берем произвольную точку L. Из фокуса F2 проводим дугу окружности радиусом АL. Из фокуса F1 чертим дугу окружности радиусом ВL, засекая первую дугу в точке М. В итоге:
АL --ВL= АВ.
Кривые второго порядка широко используются в теории и практике. В частности, они являются траекториями движения электронов.
Советуем почитать:
Проект лабораторного стенда по исследованию приемника АМ сигнала Целью данной работы является моделирование на ЭВМ части радиоприемника и создание пакета лабораторных работ по исследованию отдельных его узлов, а также создание макета лабораторно ...
Этапы проектирования печатных плат Печатная плата (на англ. PCB - printed circuit board) - пластина, выполненная из диэлектрика , на которой сформирована (обычно печатным методом) хотя бы одна электропроводящая цепь. Печ ...
Разработка конструкции и технологии изготовления модуля управления временными параметрами Современная микроэлектроника привела к революционным преобразованиям практически во всех отраслях техники, не говоря уже о радиоэлектронной и электронно-вычислительной аппаратуре. Повыше ...