В практике предшествующих дисциплин для записи динамических моделей линейных систем использовался аппарат дифференциальных уравнений. Как правило, технологические объекты управления являются системами, элементы которых имеют нелинейные характеристики и описываются уравнениями высоких порядков. В передаточных устройствах электропривода имеются люфты, возможно наличие сухого трения, приходится учитывать упругости их элементов и т.д.
Применение методов математического моделирования избавляет исследователя от решения дифференциальных уравнений, но при этом необходимо иметь аналитические модели всех звеньев.
Экспериментальные методы позволяют получить формальную модель практически любого объекта по результатам обработки экспериментальных данных. Существуют активные и пассивные эксперименты.
Активный эксперимент основан на задании объекту специально сформированных управляющих или возмущающих воздействий. По реакции объекта на эти воздействия устанавливаются и оцениваются его динамические свойства. Обычно изучается реакция на скачкообразные, гармонические или импульсные воздействия. Полученные переходные или частотные характеристики позволяют определить, например, для линейной системы передаточные коэффициенты, постоянные времени отдельных звеньев и динамические свойства объекта в целом.
Не для всех систем может быть поставлен активный эксперимент. Иногда он может быть неприемлем из-за дороговизны специального дополнительного оборудования, высокой стоимости его монтажа, нередко его реализация невозможна по условиям техники безопасности. В этих случаях применяется пассивный эксперимент. Сущность его заключается в фиксации значений входных и выходных переменных в нормальных эксплуатационных динамических режимах.
Одним из сравнительно несложных современных методов динамической идентификации, основанных на результатах пассивного эксперимента, является метод Калмана. Сущность его заключается в следующем:
- в процессе эксплуатации через строго фиксированные интервалы времени записывают значения входных и выходных параметров;
- выбирают наиболее простой вид аналитической модели, записан ной в виде разностного уравнения того или иного порядка;
- по результатам эксперимента и принятого типа модели методом минимума суммы квадратов отклонений определяют коэффициенты разностного уравнения;
- решают разностное уравнение и сравнивают полученные динамические характеристики с экспериментом;
- при больших отклонениях задаются разностным уравнением более высокого порядка и повторяют расчет.
Сопоставление изложенной выше методики динамической идентификации с порядком выполнения статической идентификации свидетельствует об их аналогии. Отличие состоит лишь в моделях: модель в ста тике описывается алгебраическим уравнением, динамическая модель — разностным.
Для дифференциального линейного уравнения k - го порядка аналогом будет разностное уравнение вида
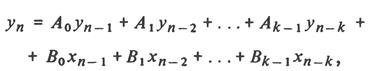
где п — номер точки эксперимента; А, В — коэффициенты разностного уравнения. Оно может быть принято в качестве исходной модели при динамической идентификации.
Поскольку порядок идентифицируемого объекта обычно неизвестен, следует начинать с наиболее простой модели, а именно — разностного уравнения первого порядка вида
![]()
Если модель окажется недостаточно адекватной, следует взять в качестве модели разностное уравнение второго порядка
yn = A0yn –1 + A0yn –2 + B0xn –1 + B0xn –2
Далее, используя методику минимизации суммы квадратов отклонений, т.е. функционала вида
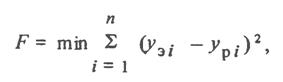
Получаем систему уравнений из которых можно А0 А1, В0, В1
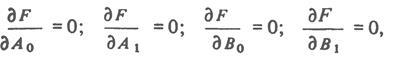
Экспериментальные модели недетерминированных объектов
Выше рассматривались простейшие случаи получения экспериментальным путем гладких, устойчиво, без разбросов повторяющихся аналитических моделей. Пригодность такой модели оценивалась по допустимому максимальному отклонению от эксперимента. На практике на эксперимент оказывает влияние действие многих малозначащих факто ров в различных непрогнозируемых сочетаниях. Поэтому при повторении опытов с одними и теми же значениями входов получают неповторяющиеся значения выходов. Разброс выходных величин, его причины и характер могут быть различными. Они могут вызываться систематическими погрешностями, являющимися функцией времени (изменение сопротивления резистора при изменении температуры, дрейф нуля усилителя и т.п.). Разброс может быть вызван пороговым действием какого-либо неучтенного фактора и при эксперименте давать повторяющуюся зависимость, имеющую характер ломаной линии. Весьма часто на разброс влияют отклонения случайного характера. Перейти на страницу: 1 2 3 4 5 6 7
Советуем почитать:
Импульсный лабораторный источник питания Для проведения лабораторных работ, исследований и испытаний приборов необходим источник питания. Требования к источникам вторичного питания, предъявляются очень высокие. Особенно к таким ...
Структурные схемы цифровых радиопередающих устройств Радиопередающие устройства (РПдУ) применяются в сферах телекоммуникации, телевизионного и радиовещания, радиолокации, радионавигации. Стремительное развитие микроэлектроники, аналогов ...
Расчет приемника наземной обзорной РЛС Основной особенностью РЭО летательных аппаратов является то, что оно работает в системе УВД, будучи связано с ней функционально или электрически. Радиотехнические средства обеспечени ...